Here is a special deck of cards. It contains only sixteen cards (The rest have been removed).
Shuffle the deck and flip over the top card 20 times. Drag the blue squares into the tally chart to keep track of how many times the top card is an Ace and how many times it is a Non-ace. (Remember to re-shuffle the deck after each draw).
Before you start…
How many times do you think the top card will be an ace? Use a drawing tool to record your prediction in the prediction box.
In this deck of 16 cards, there is an identical probability of each card being at the top of the deck. This means that each card is assigned a probability.
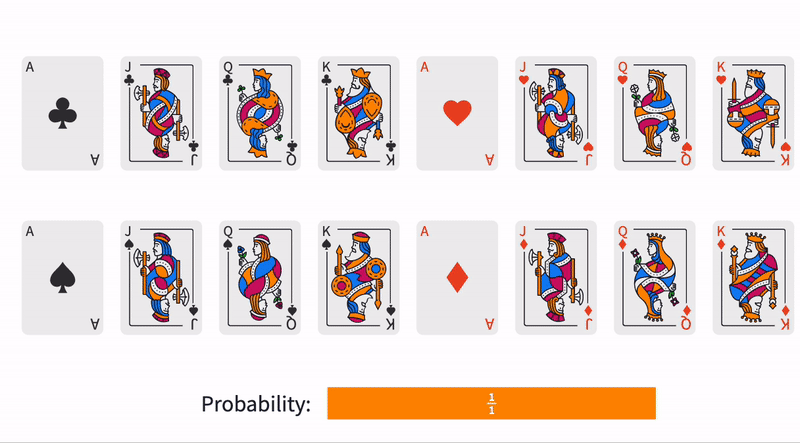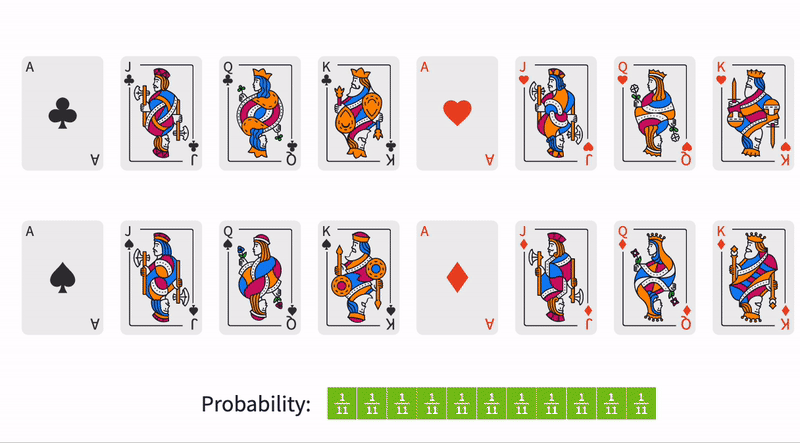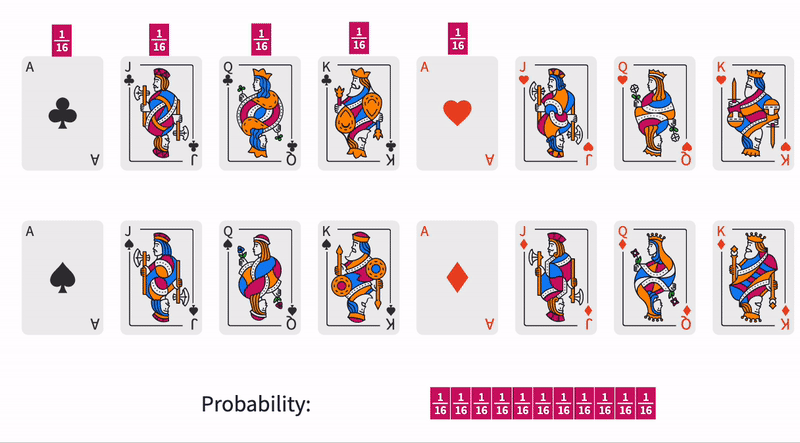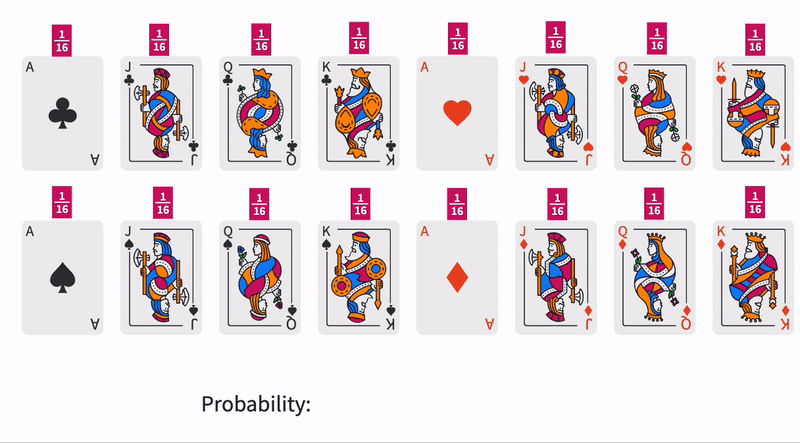
Each Ace has a probability of , but there are multiple Aces in the deck. To calculate the total probability of an Ace on the top of the deck, we must add the probability from each individual Ace.
Enter the total probability of the top card being an Ace in the Polypad below:
Since there are four aces in the deck of sixteen cards, the probability of an Ace being the top card is or .
What if we change the problem a little bit?
This time, the same 16-card deck is shuffled and the first card (we will call this "Card 1") is drawn and placed to the side. The new top card will now be called, "Card 2".

What is the probability that Card 2 is an ace?
To get started, run 20 more trials of this new experiment.
Shuffle the deck and click "draw" to move Card 1 to the side. Then select Card 2 and click "Turn over". Drag the blue squares into the tally chart to keep track of how many times Card 2 is an Ace and how many times it is a Non-ace. (Remember to replace Card 1 and re-shuffle the deck after each draw).
Before you start…
How many times do you think Card 2 will be an Ace? Use a drawing tool to record your prediction in the prediction box.
We reach a conundrum: we don't know how many aces are left in the deck after Card 1 is removed?
Unless... we cheat and take a peek at Card 1 after it has been drawn:
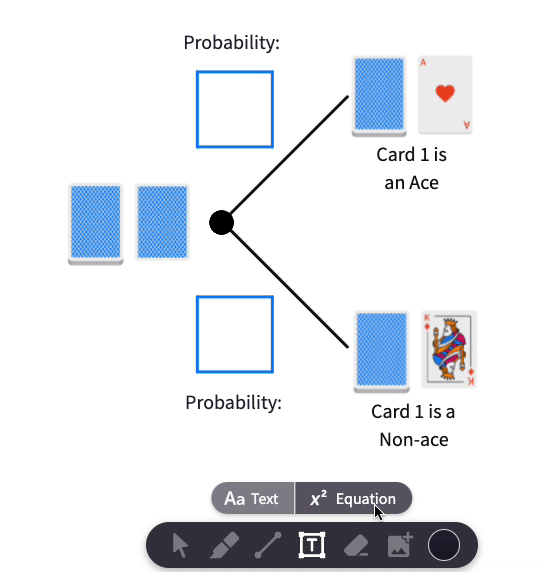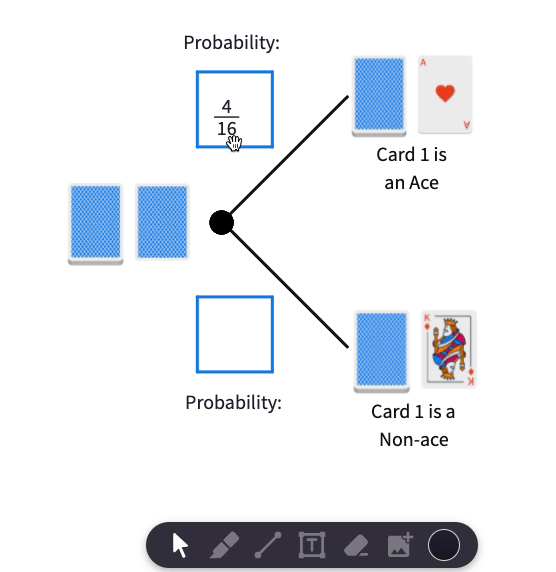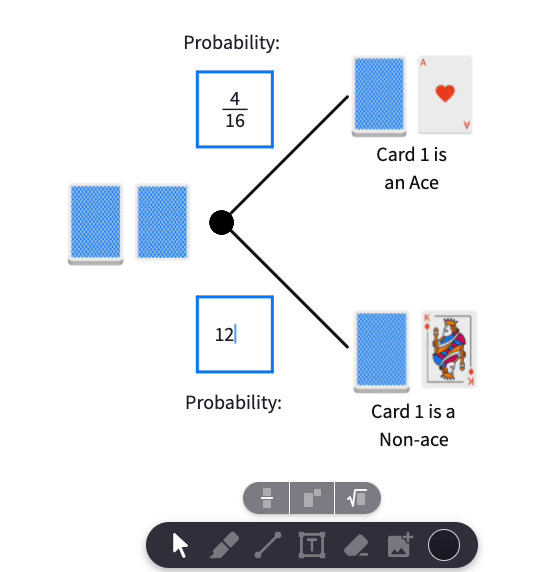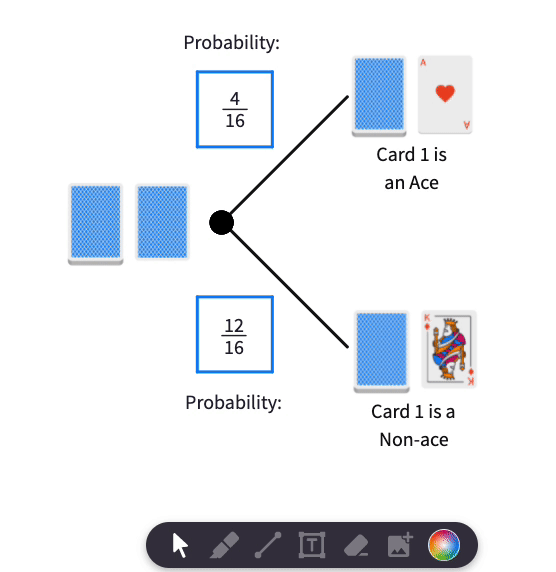
When we peek at Card 1, one of two things happens:
- Card 1 is an Ace
- Card 1 is a Non-ace.
No matter what you see, there are only 15 unknown cards left. In each situation, the new probability of Card 2 being an Ace depends on how many aces are left in the deck after you peek.
Enter the probabilities for both cases in the Polypad below.
- If we see an Ace. This means that there are only 3 aces left in the deck of 15 cards. Probability that the top card (Card 2) is an Ace falls from to or from to .
- If we see a Non-ace. This means that all 4 aces are still in the deck of 15 cards. Therefore, the probability that the top card (Card 2) is an Ace rises from to .
But we are not allowed to peek!
Instead, we must consider both timelines: One where Card 1 is an Ace and one where Card 1 is a Non-ace.
The probabilities for Card 1 look like this:
The probabilities for Card 2 look like this:
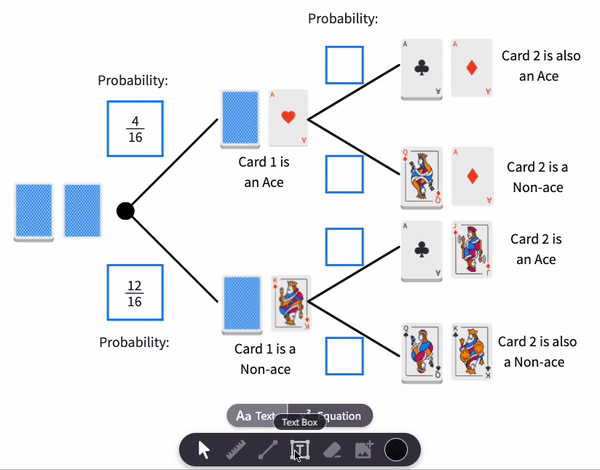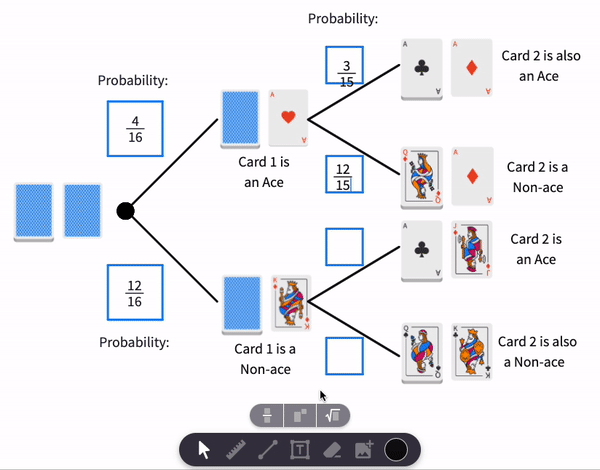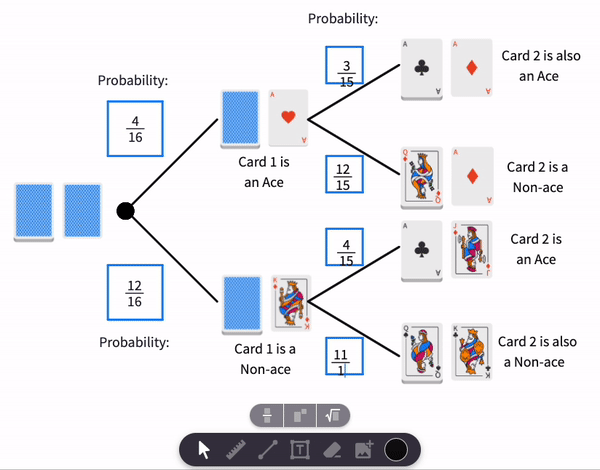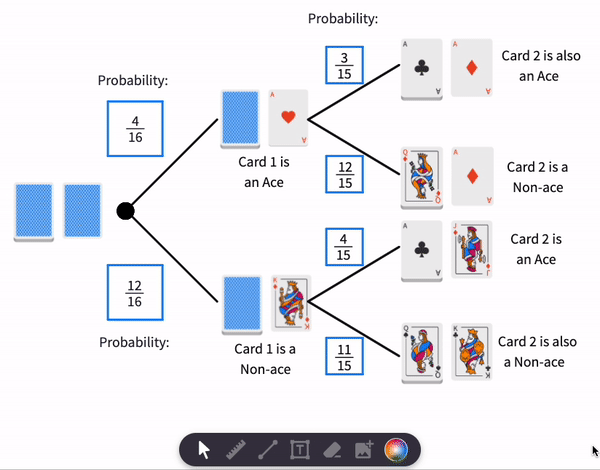
Only two of these result in Card 2 being an Ace. They are circled in blue.
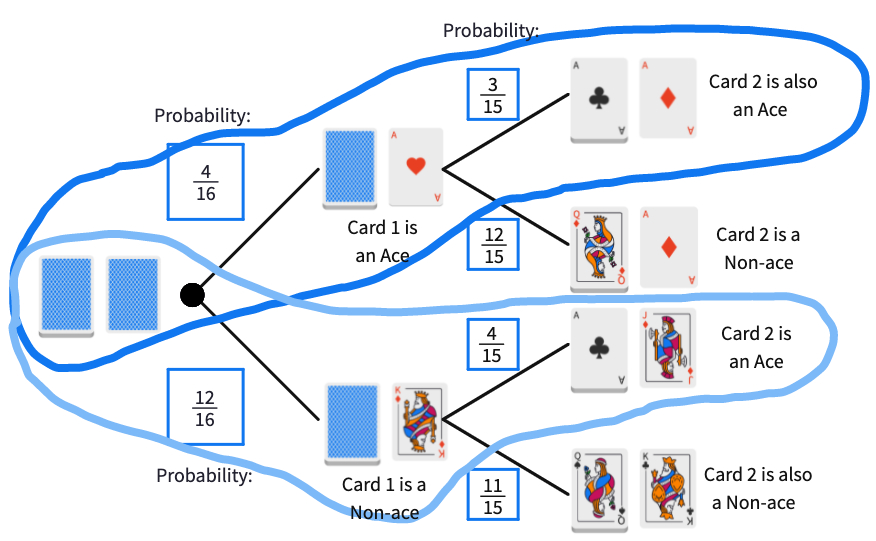
Therefore: The probability of of Card 2 being an Ace is the combination of two possibilities:
- The probability that Card 1 is an Ace and Card 2 is also an Ace.
x =
- The probability that Card 1 is a Non-ace but Card 2 is an Ace.
x =
which leads us to the final probability of:
+ = =
The exact same probability as Card 1 being an Ace!
Did your earlier trials predict this result?
Extension
What if we drew two cards without looking at them. Let's call them "Card 1" and "Card 2". The new top card will now be called "Card 3".
To get started, you might want to run 20 trials.
This exploration was inspired by: Chernoff, E. J., & Chernoff, J. W. (2015). Revealing subjective probability in the middle and high school mathematics classroom. Ontario Mathematics Gazette, 53(4), 30-35. Follow author Nat Banting on Twitter.